Nosari20
Cryptography basics

Cryptography basics

Published on: - Last update:
Url: https://nosari20.github.io/posts/cryptography-basics/

Content

Preamble

Who are Alice and Bob?

Alice and Bob are fictional characters used in cryptography to illustrate scenarios (source : Wikipedia).

The main characters are the following:

Notation

NotationDescription
$$ K_s $$Secret/Shared key
$$ K_{priv}^X $$X’s private key
$$ K_{pub}^X $$X’s public key
$$ E(K,M) $$Encrypt message M with key K
$$ D(K,C) $$Decrypt cipher C with key K
$$ S(K,M) $$Sign message M with key K
$$ V(K,M) $$Verify that M is signed with private key associated with key K
$$ h(X) $$Hash of X
$$ N_x $$Nonce (unique random number), x represents the instance

Symmetric encryption

The simplest way to share data securely is using symmetric encryption (e.g. AES). In this scenario, Alice and Bob agreed on a share key $$ K_s $$ beforehand and then encrypt the messages with it. All messages are encrypted with the same key.

Basic protocol

  1. Alice and Bob agreed on a shared key $$ K_s $$ using an already secured and authenticated channel
  2. Alice encrypts plain text $$ M $$ as $$ E(K_s,M) \to C $$
  3. Alice sends cipher $$ C $$ to Bob
  4. Bob decrypts cipher as $$ D(K_s,C) \to M $$

Limitations

  1. Alice and Bob have a secured and authenticated channel to share keys
  2. If $$ K_s $$ is leaked, Eve can decrypt all the conversations in live or afterward and Mallory can create new messages
  3. Mallory can replay some messages after being sent by Alice or Bob. This can be mitigated by using nonce to authenticate messages (first nonce sent by Alice on a secured and authenticated channel)

Asymmetric encryption

Asymmetric encryption (e.g. RSA) removes the need for a secure channel as a prerequisite for the conversation as it uses a publicly shareable key $$ K_{pub} $$ to encrypt data and a private key $$ K_{priv} $$ to decrypt data.

Basic protocol

  1. Alice and Bob share their public keys $$ K_{pub}^{Alice} $$ and $$ K_{pub}^{Bob} $$ on a public channel
  2. Alice encrypts plain text $$ M $$ as $$ E(K_{pub}^{Bob},M) \to C $$
  3. Alice sends cipher $$ C $$ to Bob
  4. Bob decrypts cipher as $$ D(K_{priv}^{Bob},C) \to M $$

Limitations

  1. Mallory can replay some messages after being sent by Alice or Bob, this can be mitigated by using nonce to authenticate messages (first non send by Alice on a secured and authenticated channel)
  2. Asymmetric encryption algorithms consume more resources than symmetric encryption ones

Hash functions

Hash functions $$ h(X) $$ (e.g. SHA)) are used to convert data of any length to a fixed length data. This operation cannot be undone by design. Plain text cannot be retrieved from hash (note: some implementations are weak, so input can be retrieved and it is possible to find multiple values for the same hash). Hash functions are used to check data integrity and in authentication processes.

Basic protocol

  1. Alice and Bob agreed on a nonce $$ N_0 $$ using an already secured and authenticated channel
  2. Alice hash plain text $$ M $$ and nonce $$ N_0 $$ as $$ h(M,N_0) \to H_{MN_0} $$
  3. Alice send plain text $$ M $$ and hash to Bob $$ H_{MN_0} $$ to Bob
  4. Bob hash received plain text $$ M_r $$ and nonce $$ N_0 $$ as $$ h(M_r,N_0) \to H_{M_rN_0} $$ and compare it to received hash from Alice
  5. If $$ H_{M_rN_0} = H_{MN_0} $$ then, this means that message $$ M_r $$ is equal to $$ M $$ and so is from Alice (the message is authenticated).

Limitations

  1. Alice and Bob have a secured and authenticated channel to share first nonce
  2. In this example, nothing is encrypted and so Eve can read everything

Digital signature

Digital signature (e.g. RSA) are used to authenticate data using asymmetric encryption keys without any authenticated channel as a prerequisite of the conversation. The sender signs data using his own private key $$ K_{priv} $$ (the data hash is signed instead of the full data), and the recipient authenticates the data received using the sender’s public key $$ K_{pub} $$.

Basic protocol

  1. Alice sends message $$ M $$ with signature $$ S(K_{priv}^{Alice},h(L)) $$ to Bob
  2. Bob receives message $$ M_r $$ and verifies that it is signed with Alice’s private key using a verification algorithm as $$ V(K_{pub}^{Alice},h(M_r) $$. If $$ V $$ returns true, then this means that message $$ M_r $$ is equal to $$ M $$ and so is from Alice (the message is authenticated).

Limitations

  1. Mallory can replay messages
  2. In this example, nothing is encrypted and so Eve can read everything
  3. Bob has to make sure that $$ K_{pub}^{Alice} $$ is really owned by Alice and not by Mallory

Protocols

Cryptographic protocols (e.g. TLS wrapp-up all the above systems to create secured and authenticated channel, they have to prevent the following attacks types (not exhaustive):

Digital certificates (aka public key certificates)

Digital certificates (e.g. x509 certificates) aim to authenticate public keys with a trust chain system (each certificate is signed by an ‘issuer’ until reaching certification authority signature which must be trusted by devices/users). A digital certificate contains multiple fields including public key, common name of the public key owner, serial number, validity and issuer identity (see example below).

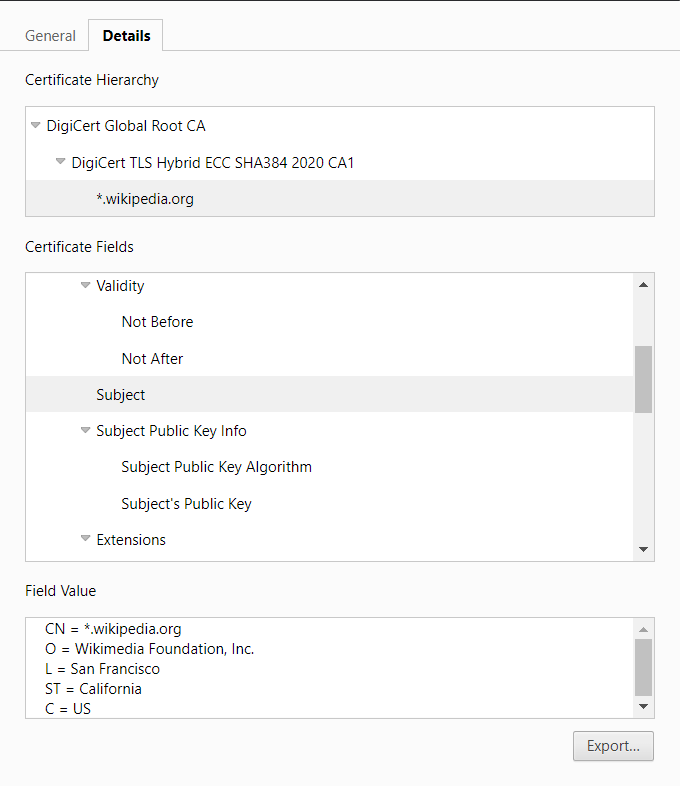
Wikipedia.org digital certificate

Common usages

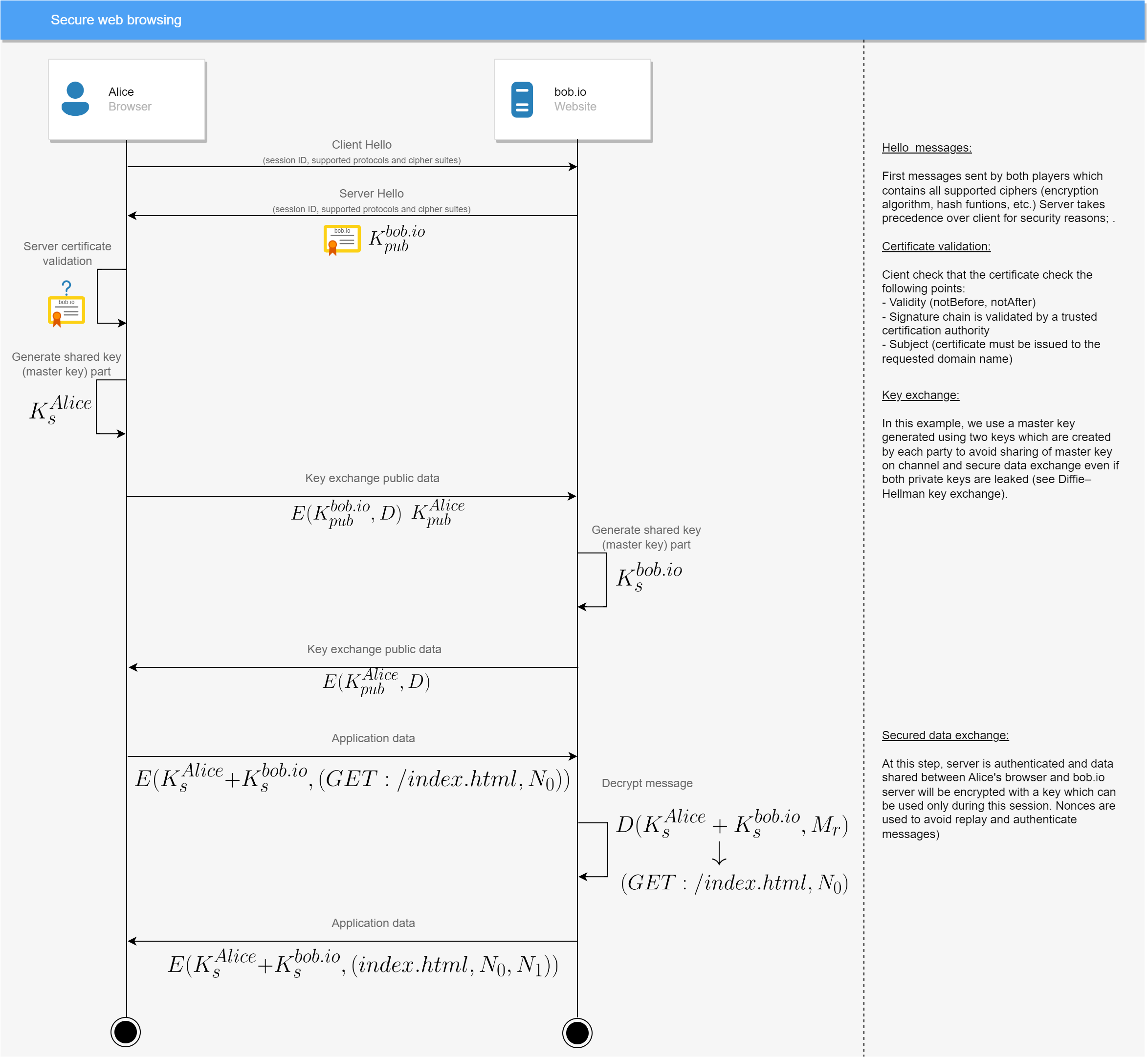
Secure web browsing

Scenario

Alice navigates to a website bob.io using HTTPS and so her browser authenticates server and encrypts data.

Prerequisites

Diagram

Secure web browsing diagram

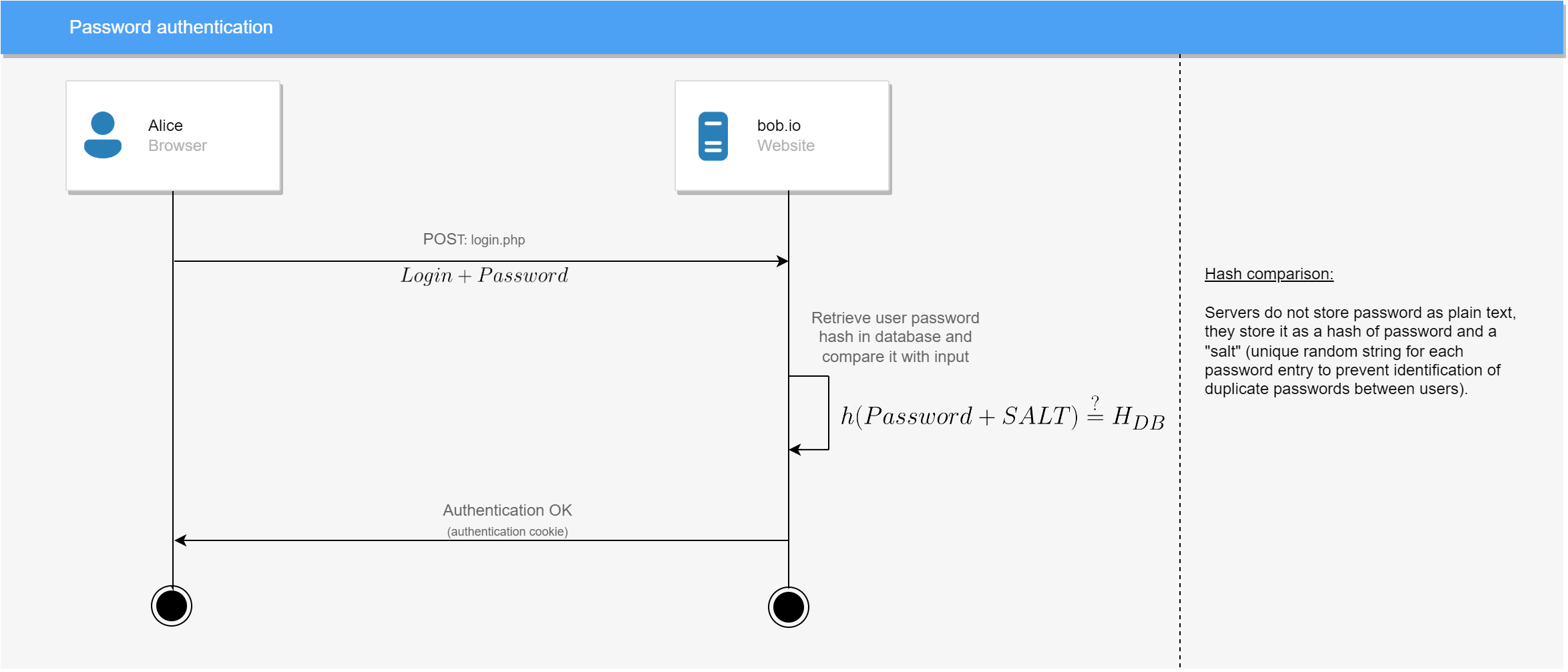
Password authentication

Scenario

Alice logged to https://bob.io using her password.

Prerequisites

Diagram

Password authentication

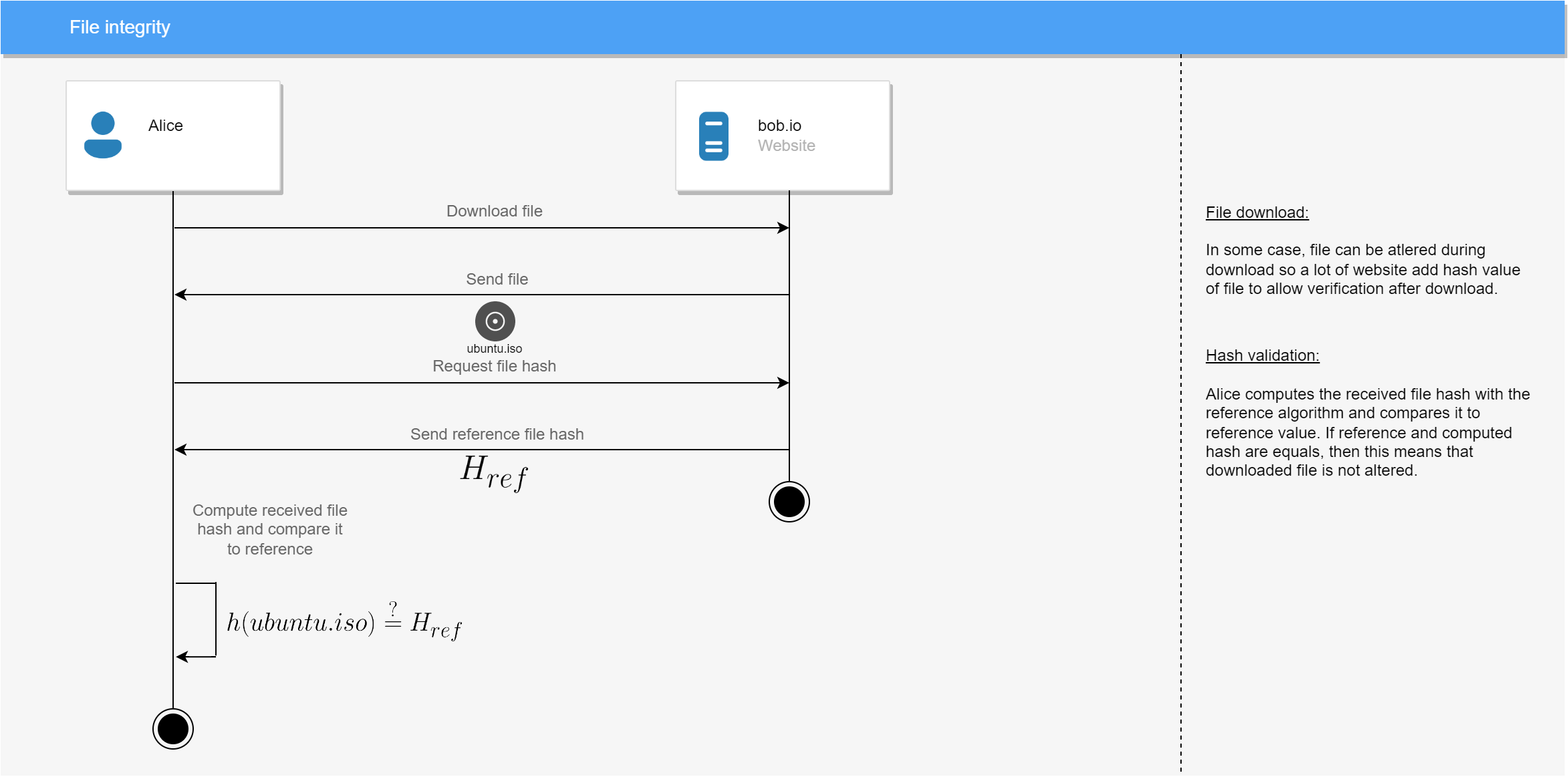
File integrity

Scenario

Alice downloads a file from https://bob.io and wants to verify the file integrity to make sure that the file was not altered during download.

Prerequisites

Diagram

File integrity check

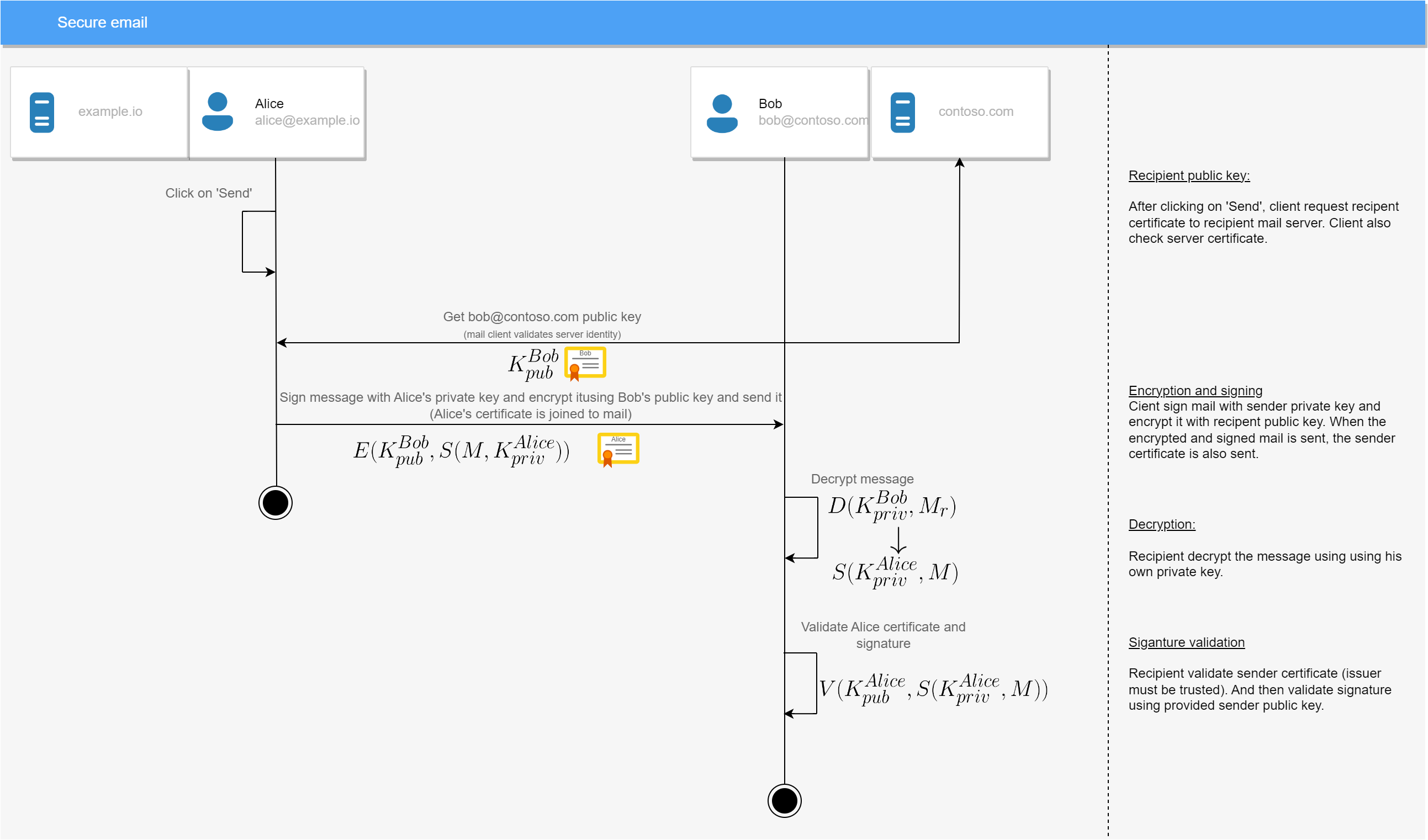
Mail signature (aka S/MIME)

Scenario

Alice sent a signed and encrypted mail to Bob (they don’t use the same mail server).

Prerequisites

Diagram

Secure email

Sources / usefull resources